Quicksort explained

This is the fifth article for the website

After reading a lot of articles on medium by Basecs, Freecodecamp,Preeti Kasireddy,and many more, I thought about trying out my hand on explaining difficult Computer Science concepts and break them down to first principles. Keeping this in mind, I will try to explain the algorithm of Quicksort in my own words.

Quicksort is a popular sorting algorithm. It has several properties that make it more desirable to use than its counterparts like Insertionsort, MergeSort or HeapSort. Its main porperties is that it is an in-place algorithm, i.e. no new data structures are created for performing the sorting. Also, it is not a stable sorting algorithm. This implies that the sorting doesn’t preserve the relative ordering of equal elements.For eg,let us consider an unsorted array:

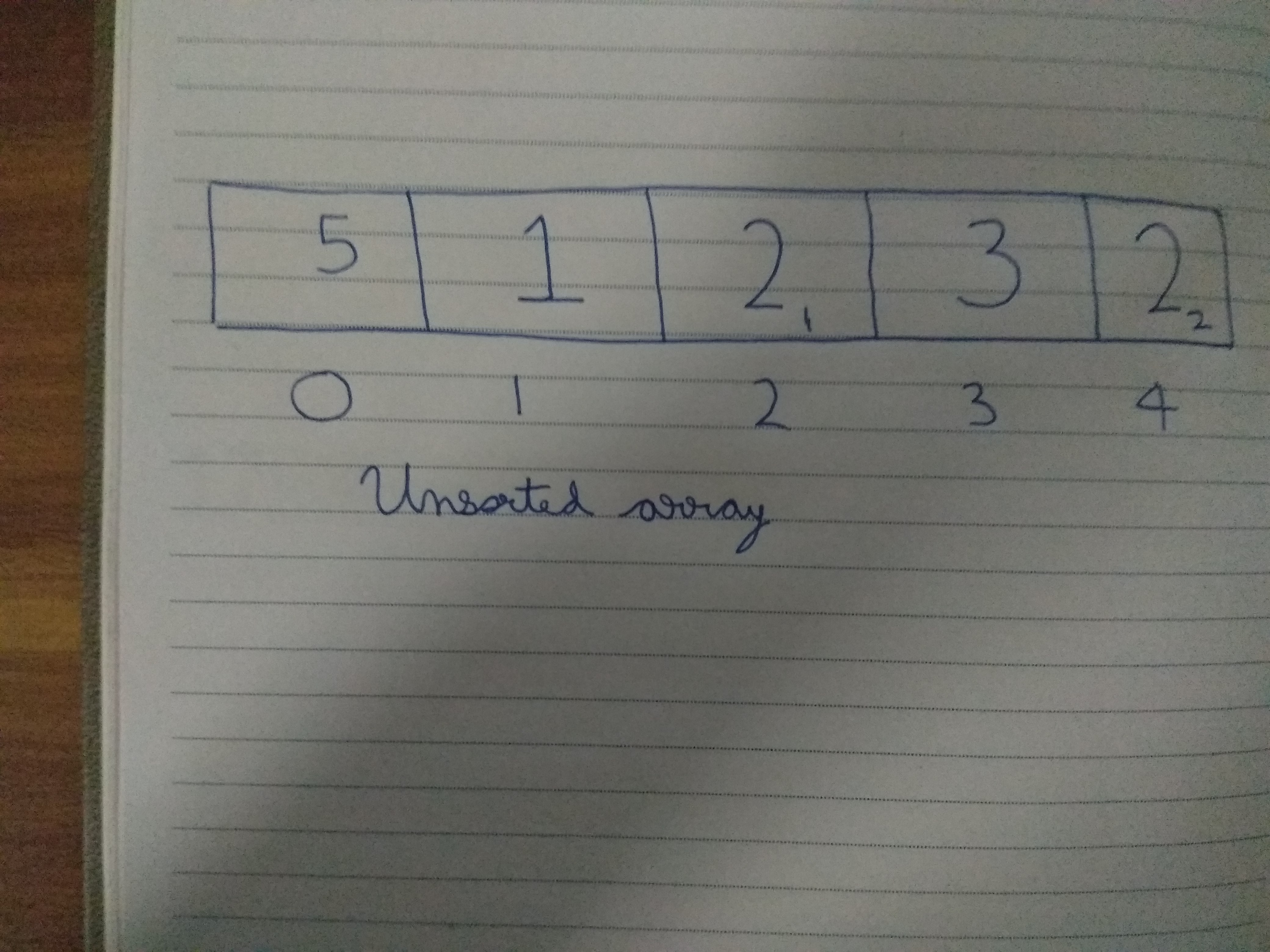
Unsorted Array

The different 2’s are identified separately as 2_1 and 2_2, depending on their order of occurence. After sorting, an unstable sort will give an array in which 2_2 can come ahead of 2_1. Quicksort is am example of an unstable sort.

So, how does quicksort work? The main element of a quicksort is the pivot element. Any element of the array can be chosen as the pivot element. By convention, pivot element can be one of the given four elements:

1. First element
2. Last element
3. Median element
4. Random element

The pivot element plays an important in the quicksort, that we will see now. We use a popular programming methodology, Divide and Conquer. In this paradigm, we decrease a problem into 2 smaller problems and divide these subproblems further into smaller sub-problems till the problem becomes very easy to solve. All these easier sub-problems are then combined together into the final problem.

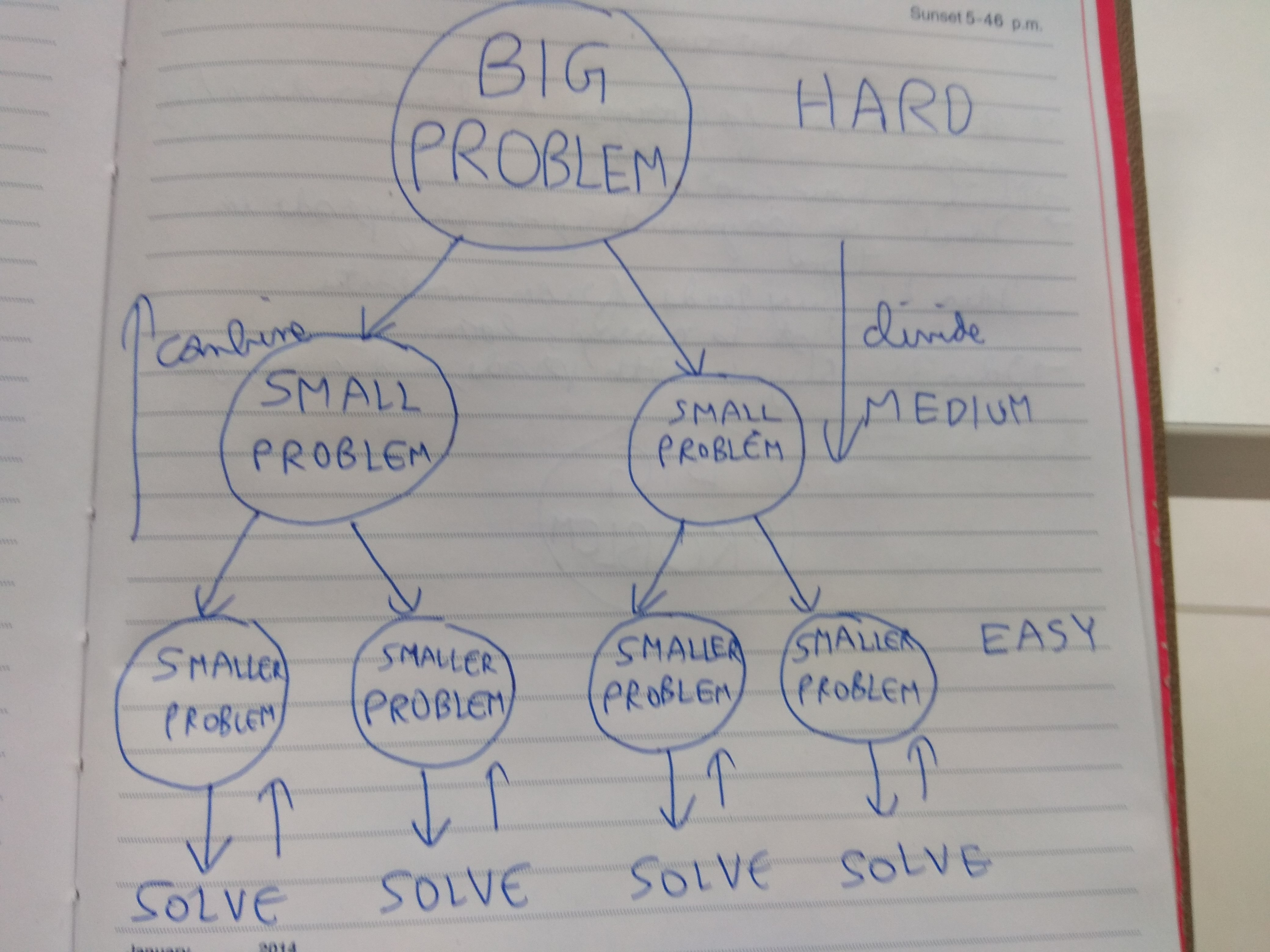
Divide and Conquer

Before delving into Quicksort, we have to understand another important method, Partition. It is an important precursor before the sorting process. In this step, we rearrange the array depending on the pivot. All the elements less than equal the pivot are put in the lower half of the array, and the remaining in the upper half of the array.

We will try to understand the working of this partition function through pseudo-code:

  pivot <- last element in array
  i <- position of lowest element - 1
  j <- index of lowest element 
  for j<- low to pivot's location - 1
    comp(a[j] >= pivot )
      i<- i+1
      swap(a[i],a[j])
  //Swap the pivot and the element in the pivot's location
  swap(pivot,a[i+1])

This is the working of the partition function:

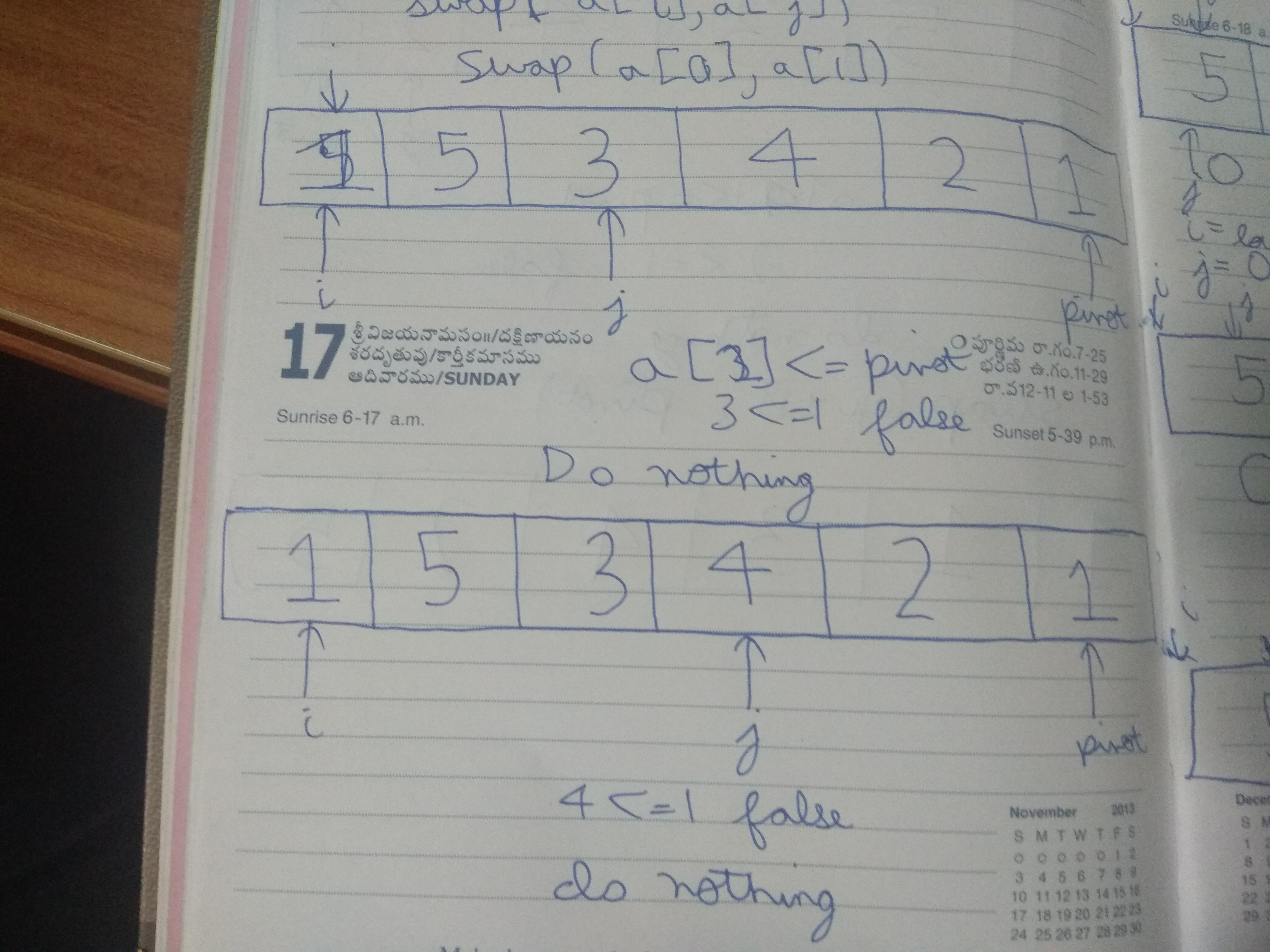
Partition step

So, after the partition step, the array is in the form: all elements <= pivot are in the lower half of the array and all the elements higher are in the upper half of the array.

Now, we can deal with Quicksort. In quicksort, as we had accounted earlier, we perform the Divide and Conquer strategy to sort the array. Divide: We perform the partition step on the lower half of the array and the upper half of the array continuously till we reach the sorted array( array with only 1 element is sorted). Conquer: Combine all the sorted arrays to form the sorted array.

The pseudocode will be:

  //Condition for recursion
  if(size > 1)
    pivot_index <-partition(array)
    quicksort(lower half of array)//Elements in the array <= pivot
    quicksort(upper half of the array)//Elements in the array > pivot

References:

1. Wikiwand article on Quicksort
2. Indian Computing Olympiad
3. Quicksort to partition the array
4. Basecs article
5. Mycodeschool video
6. Simulation of quicksort

Feel free to add suggestions in the comments below.